中点連結定理 証明
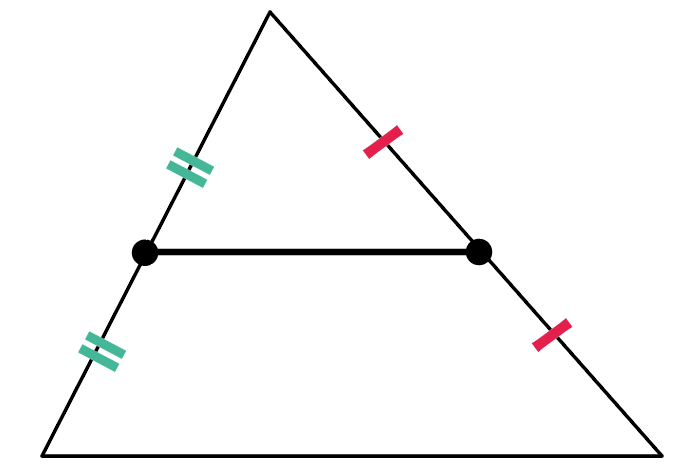
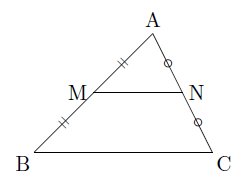
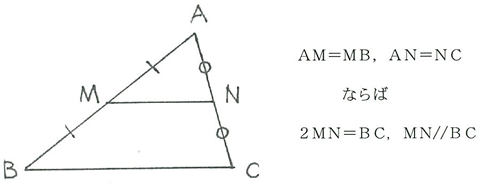
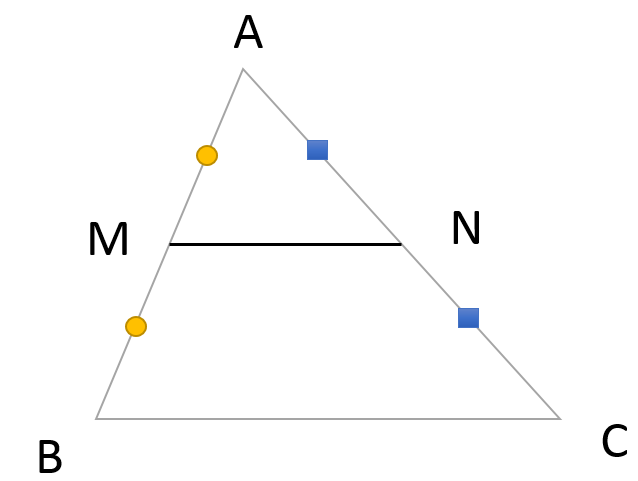
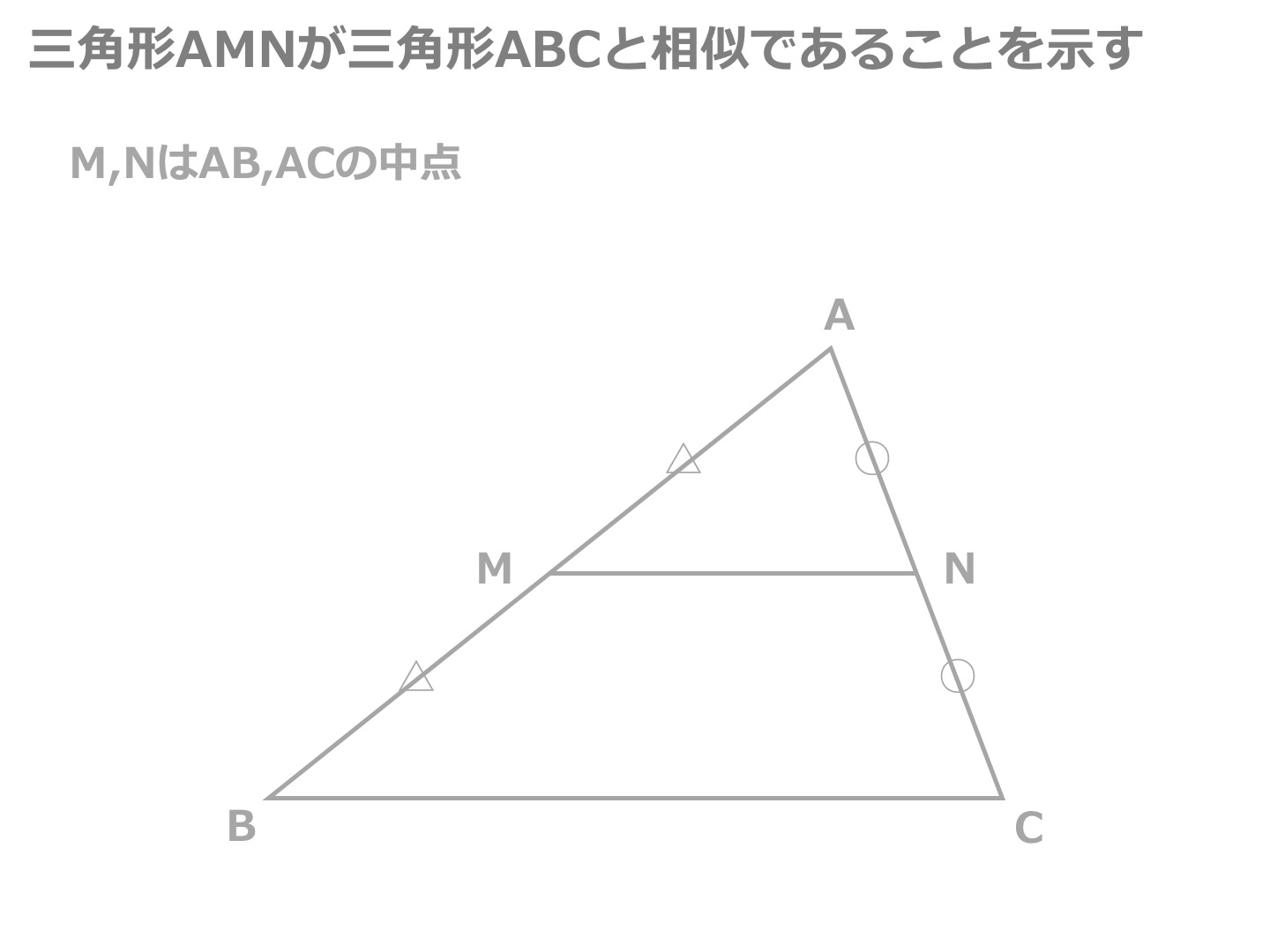
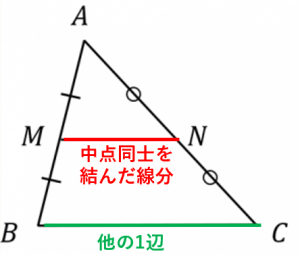
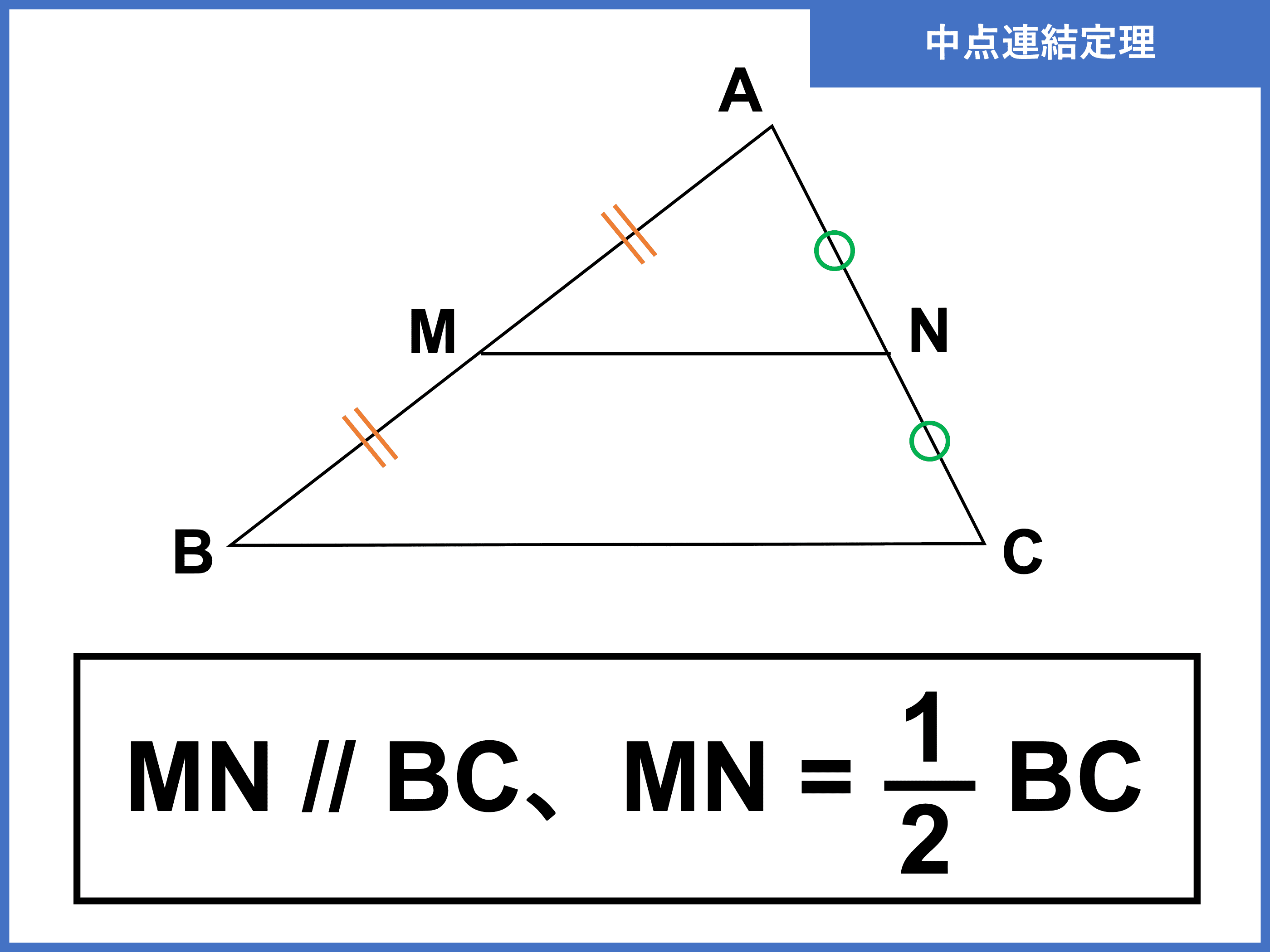
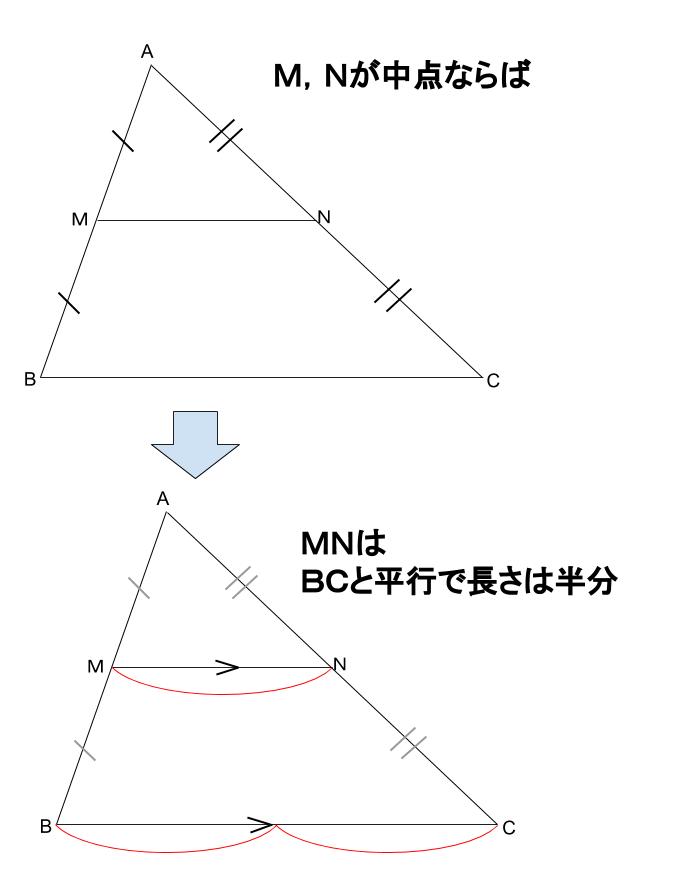
中学のときに習う中点連結定理を、ベクトルの世界で考えてみましょう。 三角形 ABC があって、辺 AB, AC の中点を、それぞれ M, N とおきます。 このとき、 MN は BC と平行で、長さが $\dfrac{1}{2}$ になる、というのが、中点連結定理の内容です。.

中点連結定理 証明. 中点連結定理とその付近の学習内容について 「大日本図書」、「教育出版」、「啓林館」、「東京書籍」、「大阪書籍」、「学校図書」の6社の 教科書を特に中点連結定理を学ぶまでの流れに着目し比較した。 以下にその内容を簡単にまとめた。. ・証明を考えさせつつ,並行して 反例も探させる。 ・対角線を引く考えを引き出す。 ・中点連結定理(①三角形,②中点)と 平行四辺形になるための条件を 教科書やノートで押さえる。 ・証明を記述させる。. これが「 対角線3等分の定理 」です。 (証明例)相似の学習の後であれば.
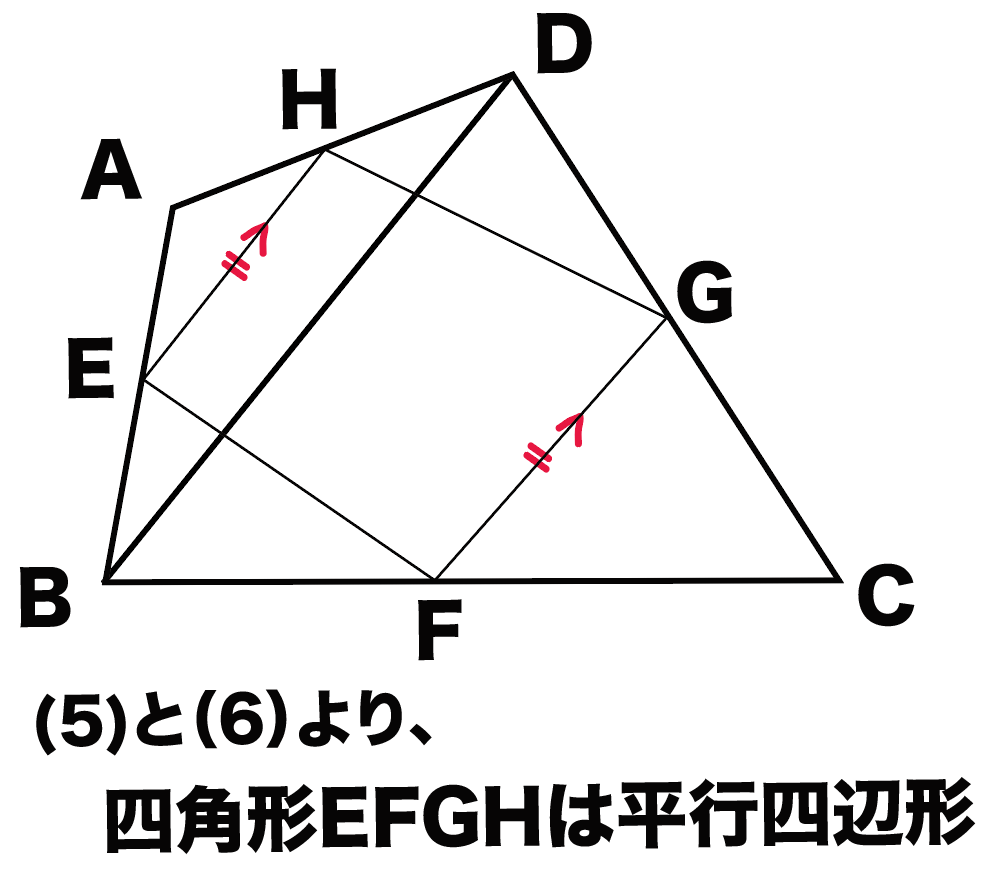
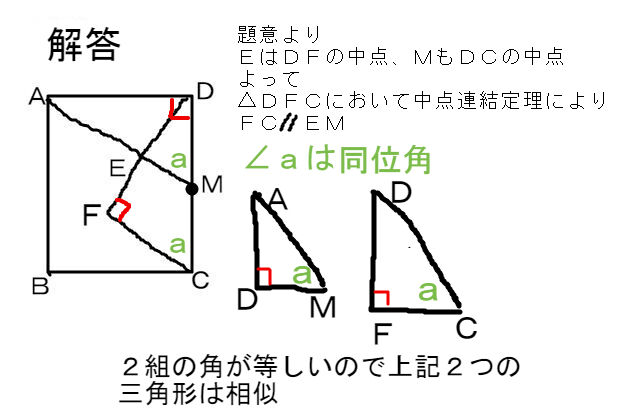
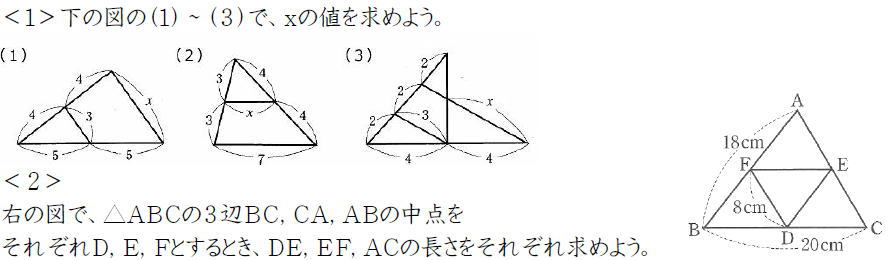
中点連結定理1−2 名前 四角形abcdで、辺ab,bc,cd,daの 中点をp,q,r,sとするとき、四角形 pqrsが平行四辺形になることを 証明しなさい。 二等辺三角形abcの頂角aの二等分線と a 底辺bcとの交点をn, 辺bcの中点をd とするとき、 danが二等辺三角形 d. A b c m n abcの2辺ab, acの中点をそれぞれm, nとすると mn//bc, mn= 1 2 bcとなる。 定理の証明 amnと abcにおいて ∠aは共通…(1) mはabの中点なのでam:ab=1:2 nはacの中点なのでan:ac=1:2 よってam:ab=an:ac=1:2…(2). Mnを延長した直線上にmn=ndとなる点dをとる。 四角形amcdで an=nc, mn=nd 対角線がそれぞれの中点で交わるので四角形amcdは平行四辺形になる。 よって.
Dとeはそれぞれ、abとacの中点ね。 中点連結定理の証明のゴールは、 de = 1/2 bc;. 参考資料 中学校新数学科の授業 第1巻~第3巻 「明治図書」 中学校新数学科授業ライブ第1学年編~第3学年編 「明治図書」. 中3数学相似な図形・第32回 中点連結定理①(証明問題)発展問題 「中点連結定理」を証明し, この定理を使い, 四角形が平行四辺形であることを証明しました。 生徒A子:「すると,この次は,この定理の逆でしょう?」 おっ,するいどい!.
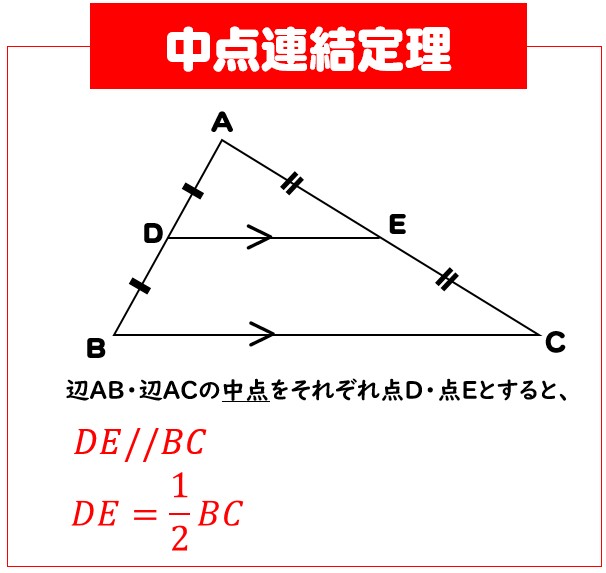
次に 中点連結定理の証明 を行います。 中点連結定理は三角形の相似を利用して比較的簡単に証明することができるので、是非自分で証明してみましょう。 中点連結定理の証明①:証明の方針. 中点連結定理 abc で,2 辺ab,ac の中点を,それぞれ,m,n とすると mn // bc ,mn =bc がいえる。これを中点連結定理という。 これは,特に新しい内容ではありません。「5線分の比と平行線」で比が 等しいと平行になることと,その証明の途中で三角形が相似. Try IT(トライイット)の中点連結定理を使う証明の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の.
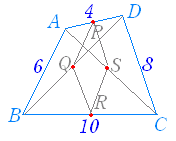
中点連結定理の証明 では、次に中点連結定理の証明について解説していきます。 相似な三角形の性質 を利用して、中点連結定理を証明します。. C726Q_T_045-058.smd Page 12 17/09/15 16:28 v3.10 別の方法で証明してみよう 31 ページで学習した中点連結定理 茨ABC の2 辺AB,AC の中点を, それぞれ,M,N とすると, MN科BC,MN= 1 2 BC について,平行四辺形の性質を使うと,次のように証明することができます。. まず,$4$ 点 $M_B,M_C,E_B,E_C$ がある円 $\Gamma$ 上にあることを中点連結定理を用いて示します. つぎに,$H_B,H_C$ も円 $\Gamma$ 上にあることを円周角の定理などを用いて示します..
中点連結定理 中点連結定理は、三角形の頂角をはさむ \(2\) 辺上にそれぞれ \(2\) つの中点をとるとき、『中点を結ぶ直線と三角形の底辺は平行で、中点を結ぶ直線の長さは底辺の長さの半分になる』というものです。 定理の証明. まずは adeと abcの相似 の証明だ。 d・eはそれぞれの中点だから、 ad=db;. 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方の定理の証明(2) 三平方の定理の証明(3) 三平方の定理(1) 三平方の定理(2) 三平方の定理の逆:.
中点連結定理 中点連結定理の概要 ナビゲーションに移動検索に移動この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(16年10月) 中点連結定理。辺 mn と b. 定理 :数学の命題の中で,正しいと証明された もののうち,特に重要なもの (例)中点連結定理 証明 :定義と公理に基づいて,命 題が正しいことを論理的に示すこと 定義 :言葉の意味,用法を規定すること. 数学Ⅰ1.数と式 展開公式・因数分解公式+α 絶対値の性質・方程式・不等式 平方根の性質・2重根号2.2次方程式・2次関数 平方完成 2次方程式の解・重解・解の個数 関数の平行移動・対称移動3.図形と計量 正弦定理・余弦定理 $90^{ \.
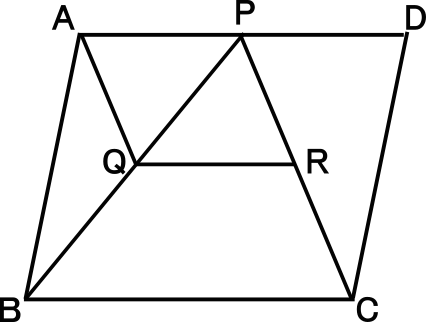
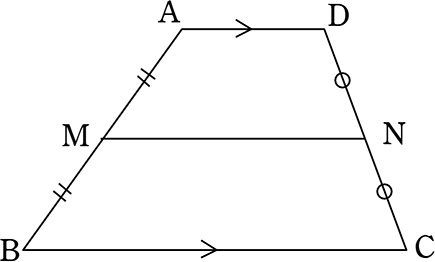
このとき、三角形 abc の中点連結 mn は、底辺 bc と平行であり、かつ 中点連結 mn の長さを 2 倍すると、底辺 bc の長さに等しくなることを示し、中点連結定理が成り立つことを証明する。. ※MはABの中点 NはDCの中点 AD//BC であることがわかっています。 又はPがACの中点である証明 でもかまいません。 いずれにせよ MN//BC、PがACの中点であることがわかっていないと 中点連結定理は利用できないと思うのですが….
中3数学 2分でわかる 中点連結定理とは Qikeru 学びを楽しくわかりやすく
中点連結定理とは 証明 問題の解き方の解説 数学fun
Q Tbn 3aand9gcqpjawhhuxw7soeoupv8vc34gjqqhx9duhcnhqbhtjyiqgthcyz Usqp Cau
中点連結定理 証明 のギャラリー

中学数学3 中点連結定理の証明 中学数学 By となりがトトロ マナペディア

中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ

中点連結定理を利用した証明 チーム エン
中学数学 図形の相似

三角形の角の二等分線と線分の比 個別指導学院core コア 西川口の個別指導塾

中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ
Mathematics 相似 5 中点連結定理と重心 働きアリ The 2nd
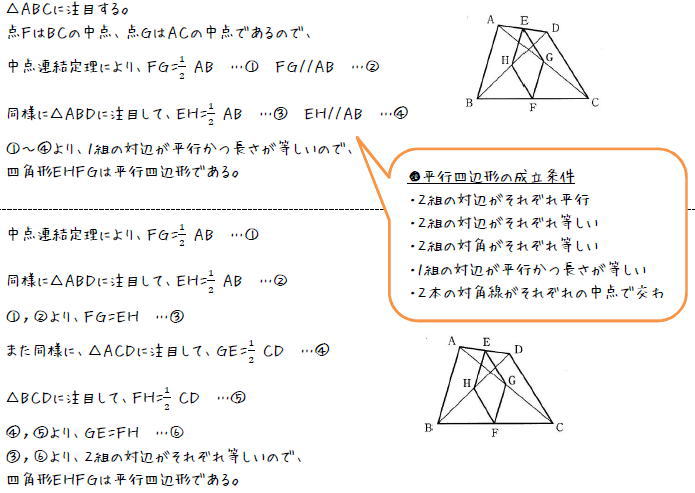
Studydoctor中点連結定理の利用 中3数学 Studydoctor

中点連結定理の問題 中学数学に関する質問 勉強質問サイト

初等幾何学から4 中点連結定理 身勝手な主張
Q Tbn 3aand9gcswui1w2vpuv5lrnapeqjrzwgbjxhbcqnry Qqskmvqafsyhdpi Usqp Cau
中点連結定理 まなびの学園

中3数学 中点連結定理ってどんな定理 Cafeducation

中点連結定理 思考力を鍛える数学

中点連結定理 例題 きっずゼミ子育て応援ブログ
Http Www City Hadano Kanagawa Jp Www Contents Simple C064 Pdf
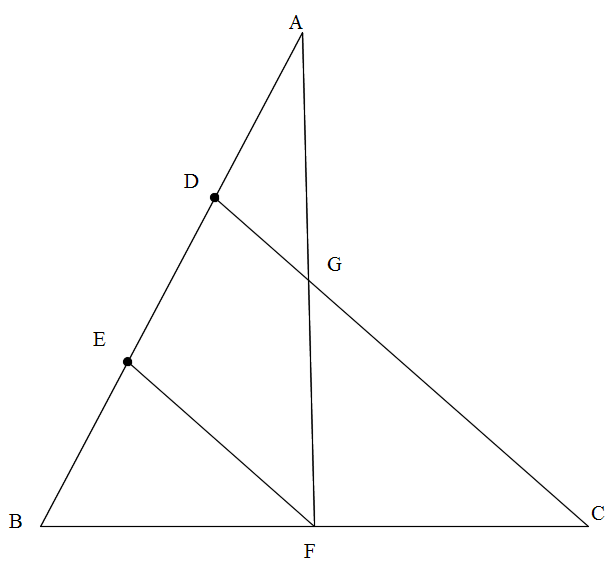
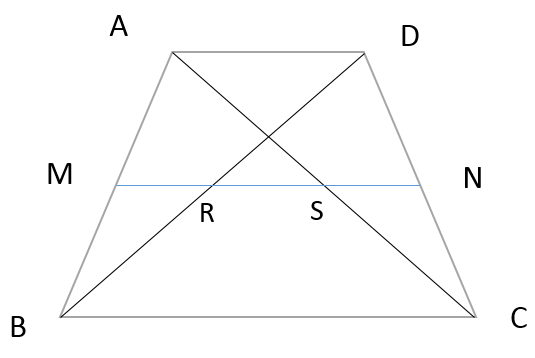
中点連結定理 中学入試 高校入試 算数 数学質問所

中3数学 中点連結定理とは 練習編 映像授業のtry It トライイット
中学数学 中点連結定理 三角形 四角形 台形 行け 偏差値40プログラマー
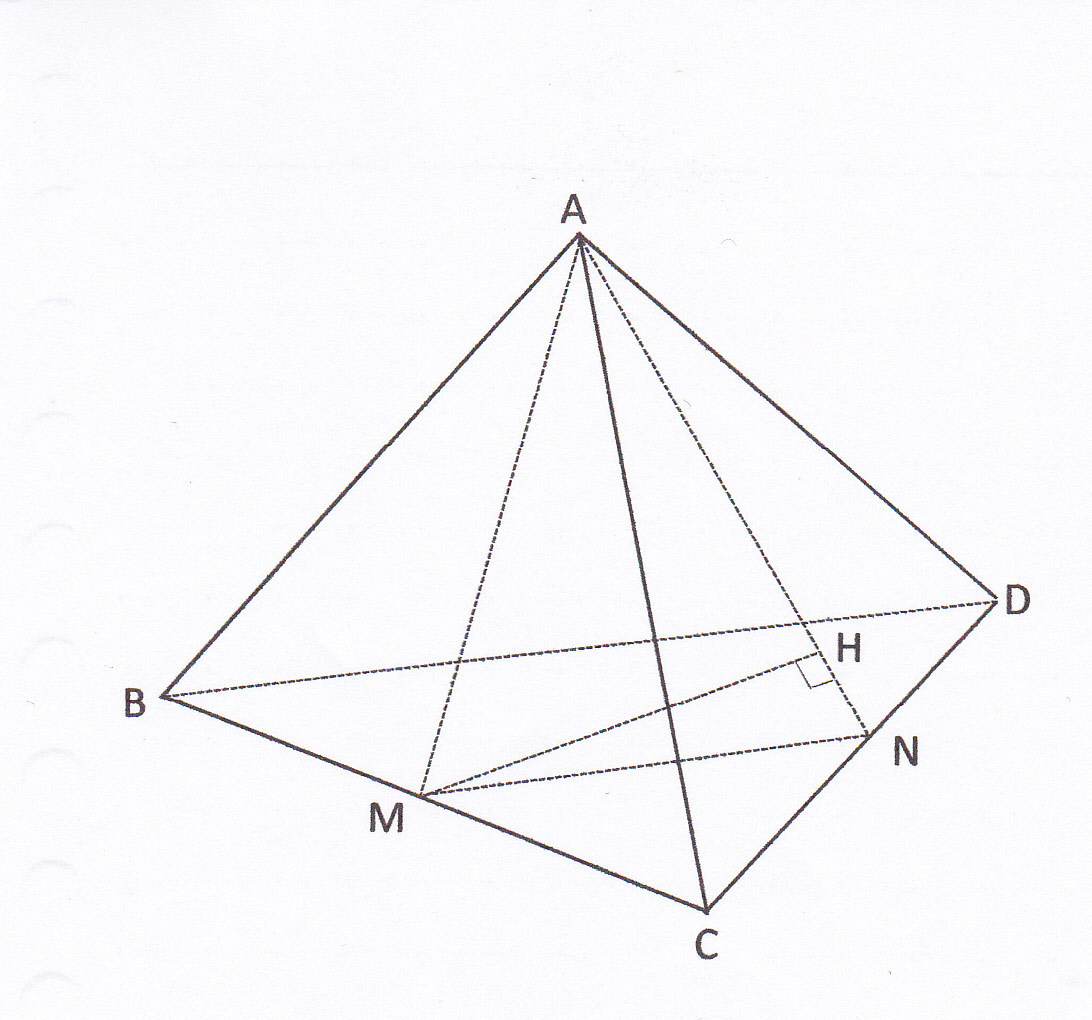
三平方の定理 中点連結定理と空間図形の融合問題の解き方 現役塾講師のわかりやすい中学数学の解き方
中学3年数学練習問題 中点連結定理 図形と相似
中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
Q Tbn 3aand9gcqa48sfdjgrrdna9rj90flffp3ulx9wompz6gfdnnca5nyih57s Usqp Cau

中点連結定理ってどんなときに使えるんですか 教えてください Clear

中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ
第178回 数学 三角形をさがせ 解答 解説 家庭教師が伝授する具体的な成績アップの勉強法と秘訣を公開
中学数学 図形の相似
中点連結定理1

中学数学の中点連結定理を使う初等幾何学の問題を1問解こう 身勝手な主張
中学数学 中点連結定理 三角形 四角形 台形 行け 偏差値40プログラマー

中学生 中点連結定理のノート一覧 Clear
三角形 中点連結定理 入試正答率4 の問題 中学数学 寺子屋塾の復習サイト

中3数学 中点連結定理を使う証明 練習編 映像授業のtry It トライイット

中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ
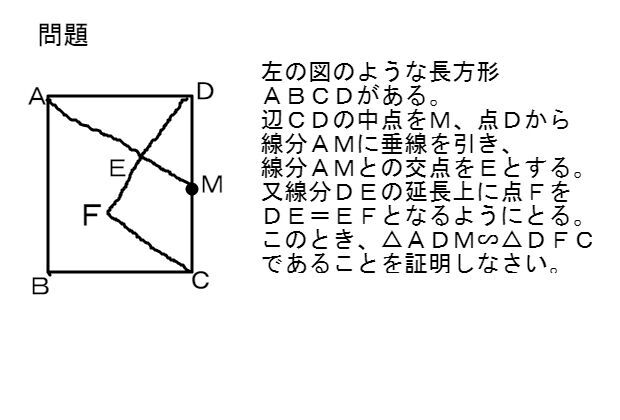
三角形 中点連結定理 入試正答率4 の問題 中学数学 寺子屋塾の復習サイト

中点連結定理 無料で使える中学学習プリント

中3数学 中点連結定理ってどんな定理 Cafeducation
3分でわかる 中点連結定理の証明 問題の解き方をわかりやすく 合格サプリ

質問 数学a 図形 三角形に外接円が必ず存在する理由 オンライン無料塾 ターンナップ

中点連結定理 中学数学に関する質問 勉強質問サイト
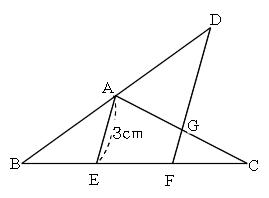
Mathematics 相似 5 中点連結定理と重心 働きアリ

中点連結定理 身勝手な主張
中点連結定理とその逆の証明および例題 具体例で学ぶ数学

三角形の重心の問題です 数学 算数のq A 解決済み Okwave

これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear
中点連結定理とは 証明 定理の逆や応用 問題の解き方を簡単に解説 受験辞典

Mathtriangleの雑記帳

中点連結定理を使った証明 Youtube
中点連立定理を考えよう

数学a 図形の性質 以下の問題の解説赤線部について 相似条件は 3辺が等しい Clear

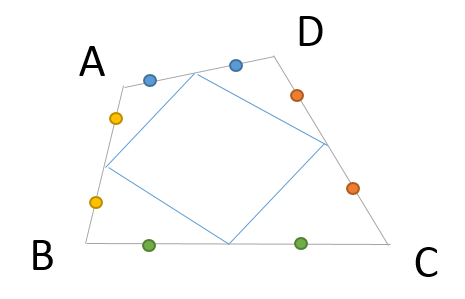
中点連結定理の利用で 以下の図形の中点を結ぶとどんな四角形ができるか またその証明を Clear
授業実践記録 数学 新しい 定理 とその活用 啓林館
中学3年数学練習問題 中点連結定理 図形と相似
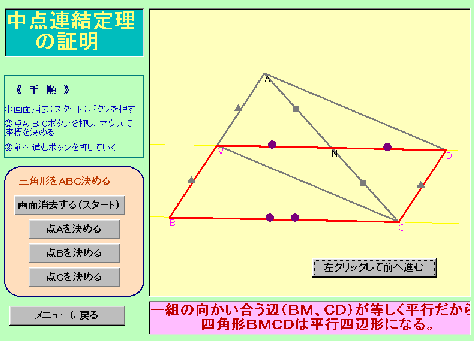
中点連立定理を考えよう

中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ

中点連結定理証明 写真共有サイト フォト蔵
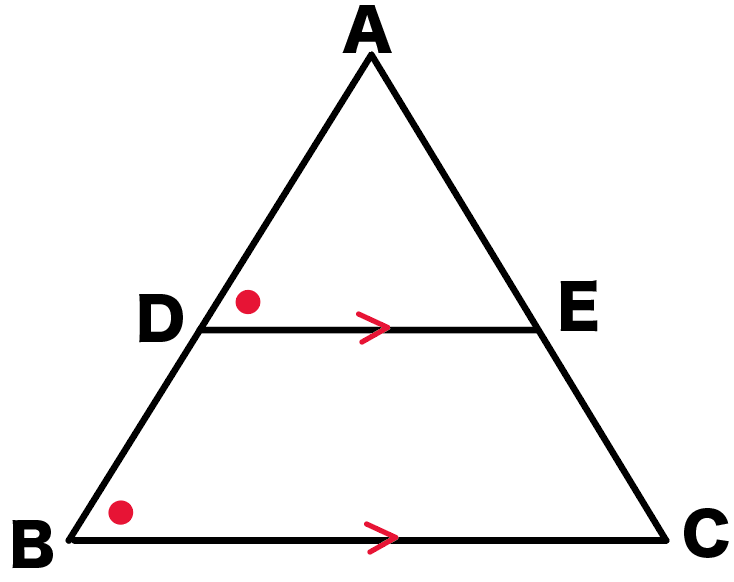
中3数学 中点連結定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく
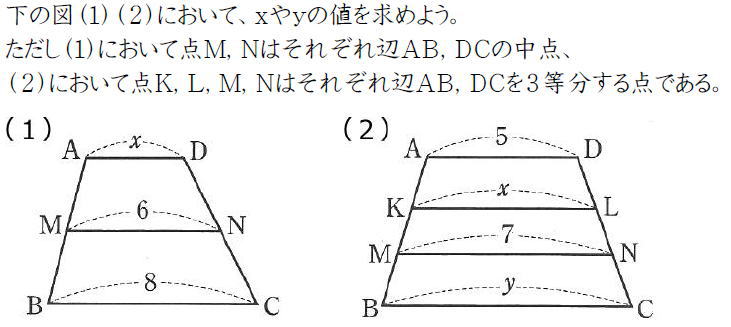
Studydoctor台形と中点連結定理 中3数学 Studydoctor
Q Tbn 3aand9gcr Xdqze1owcluktm7c Gdsd6xyuxmzbtgx 8kn3g Rsqrgpo4q Usqp Cau
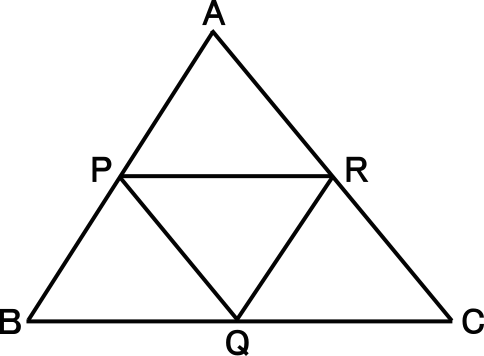
中学3年数学練習問題 中点連結定理 図形と相似

無料 中3数学 基本解説 解答プリント 図形の相似4 中点連結定理 縮図

これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear

中3 平行四辺形と相似 中点連結定理 Youtube
中学数学 中点連結定理 三角形 四角形 台形 行け 偏差値40プログラマー

中点連結定理の一証明 身勝手な主張
中学数学 中点連結定理の証明と問題 台形にも使える便利な定理 Studyplus スタディプラス

中3 中点連結定理の証明です やり方も教えてください Clear

中線定理の3通りの証明 高校数学の美しい物語

中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学

台形と中点連結定理 数学 算数のq A 解決済み Okwave

中3数学 中点連結定理ってどんな定理 Cafeducation

初等幾何学から4 中点連結定理 身勝手な主張

中3数学 中点連結定理ってどんな定理 Cafeducation
中学数学 中点連結定理 中学数学の無料オンライン学習サイトchu Su
Studydoctor中点連結定理 中3数学 Studydoctor

三角形の重心の性質とその証明 求め方 数学a By となりがトトロ マナペディア

質問 Itmedia 台形と中点連結定理
定理5

中3数学 中点連結定理を使う証明 映像授業のtry It トライイット

中点連結定理 Wikipedia

初等幾何学から4 中点連結定理 身勝手な主張
中学数学 中点連結定理の証明と問題 台形にも使える便利な定理 Studyplus スタディプラス
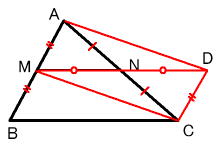
中点連結定理の証明

中3数学 中点連結定理を使う証明 例題編 映像授業のtry It トライイット

数学 中3 51 平行線と線分の比 中点連結定理編 Youtube

三角形の重心の性質とその証明 求め方 数学a By となりがトトロ マナペディア

中点連結定理 問題 Youtube

中点連結定理に関する質問 勉強質問サイト
中学数学 中点連結定理の証明と問題 台形にも使える便利な定理 Studyplus スタディプラス

中点連結定理 中学数学に関する質問 勉強質問サイト

中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ

中点連結定理の利用で 以下の図形の中点を結ぶとどんな四角形ができるか またその証明を Clear

中点連結定理 チーム エン
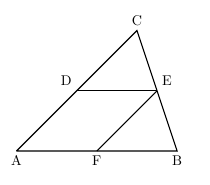
中点連結定理の問題の解法 夢を叶える塾
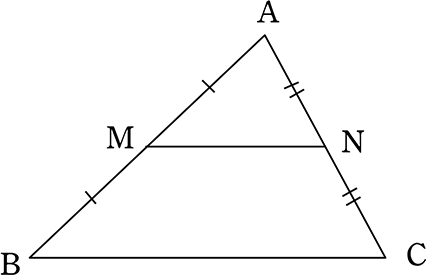
中学数学 図形の相似

中3数学 中点連結定理ってどんな定理 Cafeducation

中点連結定理の一証明 身勝手な主張
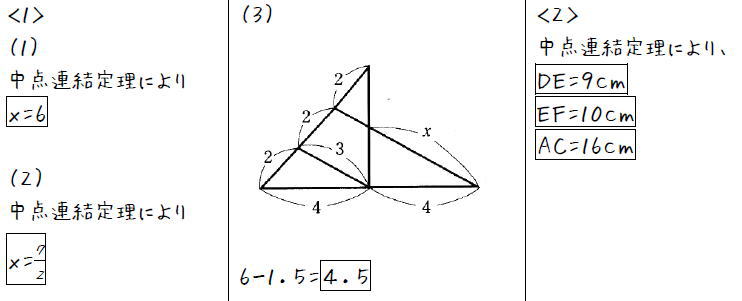
Studydoctor中点連結定理 中3数学 Studydoctor
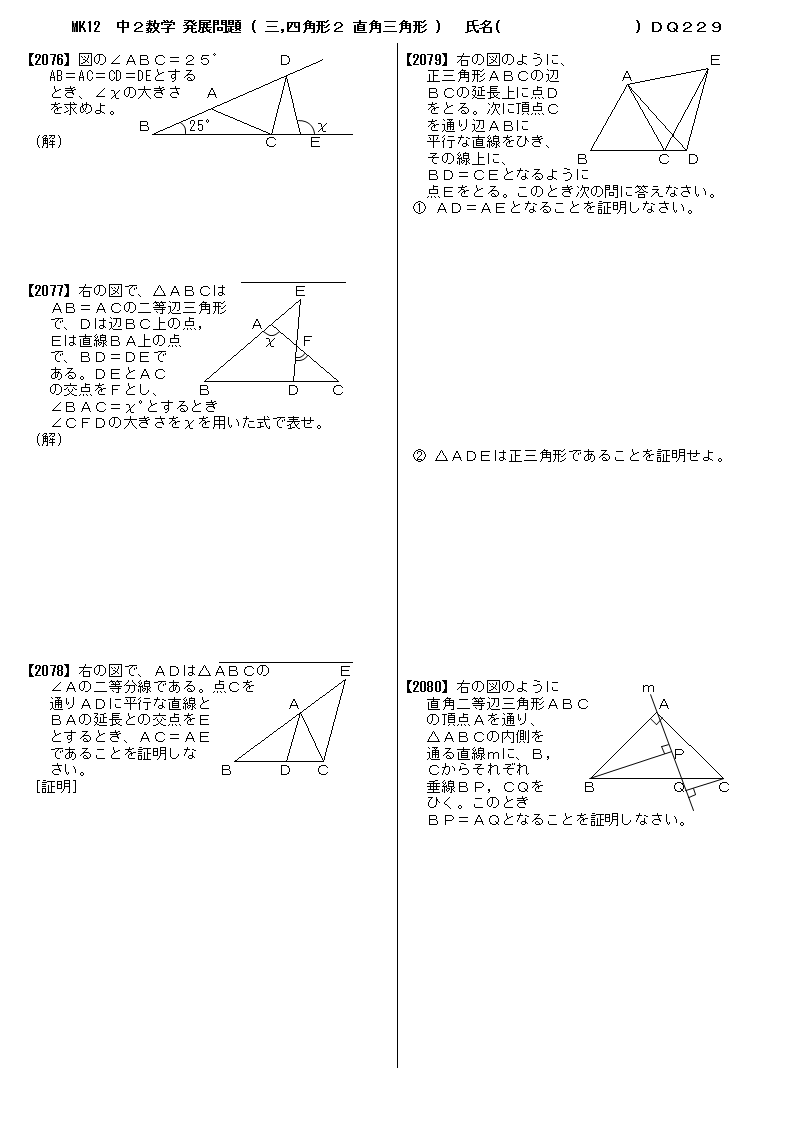
無料 中2数学 応用 発展問題 問題プリント 329 図形の相似4 中点連結定理

中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ
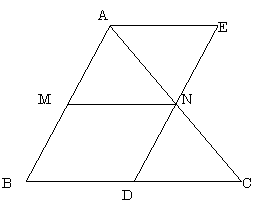
中点連結定理の証明



